この記事は理情 Advent Calendar 2024 - Adventar の9日目の記事として書かれました。

前回はtaka2さんの記事でした。

はじめに

一之瀬、Segtree、TAISAの３人で「頂点被覆バトル」を行った。

「AIじゃんけん大会 - Segtree’s blog」に引き続き、ゆるくプログラムを書いて遊ぼうという会である。

今回の提案は私で、大昔のAtCoderオンサイトでグラフ彩色問題に対して同様のものがあったと聞いたため、それにヒントを得た。

ルール

頂点被覆問題に取り組む。

各プレイヤーは、solver（グラフが与えられたときに、できるだけ小さな頂点被覆を返すプログラム）と、テストケースとその想定解（グラフとその頂点被覆の例）をひとつづつ作る。

総当たりで各solverに各テストケースを入力として与え、solverの解と想定解の頂点の数の差分が各プレイヤーの得点/失点になる。例えば、プレイヤーAのsolverにプレイヤーBのテストケースを与えたときに、プレイヤーAのsolverの解が4000頂点、プレイヤーBが作った想定解が3000頂点だった場合には、プレイヤーAに-1000点、プレイヤーBに1000点が入る。この総和で順位を決める。

グラフのサイズは N, M <= 10000 で、実行時間はその場の気分で決めることになった。

solver

一之瀬

各頂点について「必ず選ぶ」「選んでも選ばなくてもよい」を決め、これに関して山登りを行う。「選んでも選ばなくてもよい」とした頂点集合による誘導部分グラフに対して、葉があれば切った上で、貪欲法を行ってスコアを計算する。

Segtree

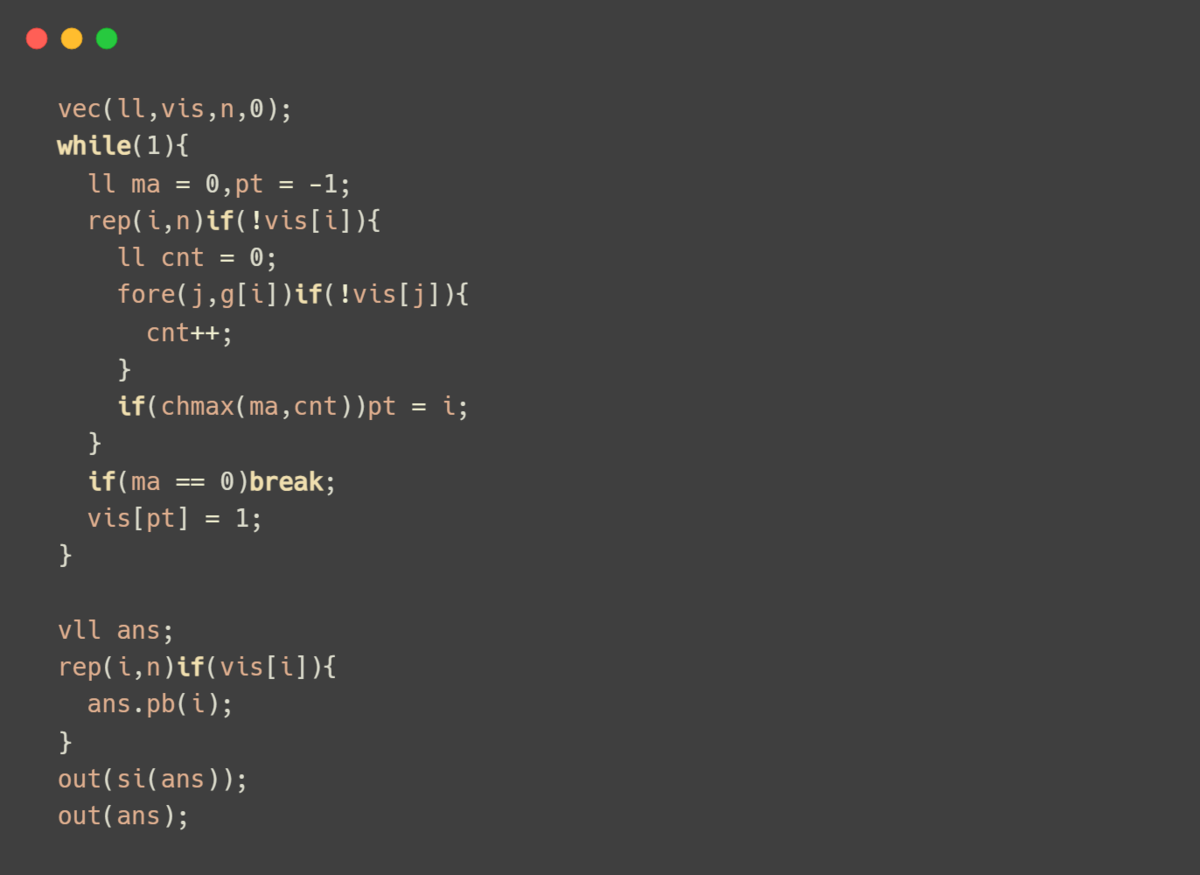
単純な貪欲法。

「次数の大きな頂点を頂点被覆に追加し、それに隣接する辺を削除する」ことを繰り返す。

葉を切っていくなどの他の愚直なヒューリスティックでも落ちない反例がそこまで自明ではなかったので、これを落とすのはそこそこ大変だろうと思ってこのまま投げた。

TAISA

極大マッチングを使った2近似アルゴリズムを実装していた。

辺を見る順番によって解が変わるが、この順を山登りしていた。

testcase

一之瀬

N=7129, M=10000

想定解：3565

貪欲キラーを何時間かプログラムを回して生成したらしい。

zenn.dev

・vs. Segtree（solver）

4409 (+844)

・vs. TAISA（solver）

4568 (+1003)

狙い通りしっかり貪欲法に対策ができており、貪欲法的なアプローチをしていたsolver側に対して1000近い差を生み出すことに成功していた。

Segtree

N=6875, M=9999

想定解：3125

以下のように、11頂点15(+1)辺の小グラフを繋げたものである。

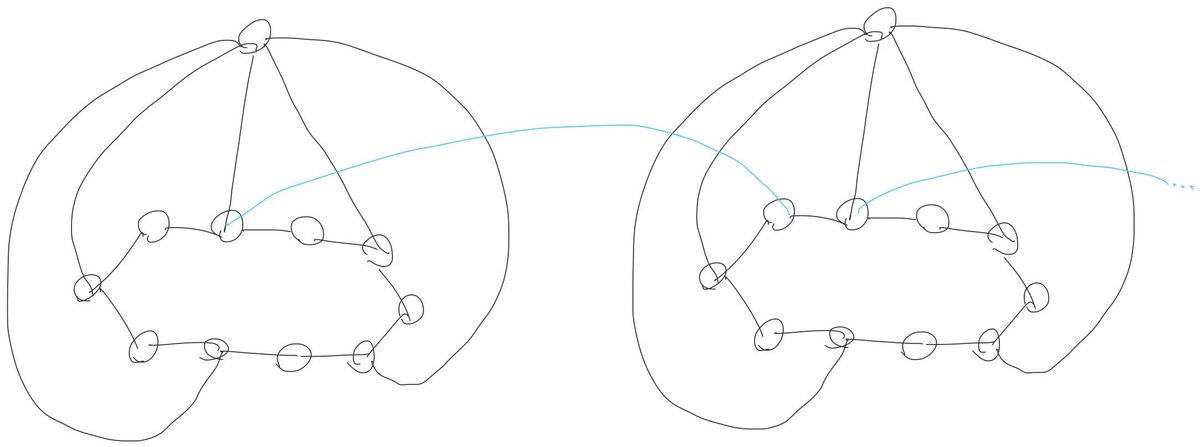
各小グラフは、自分の書いた「次数が大きなものから取る」という貪欲法に対するキラーケースになっている。輪の部分の10頂点から上の1頂点に繋がっている5つを取れば頂点被覆になっているが、貪欲法では上の頂点も取って6つを取ることになり、差が生み出せる。

・vs. 一之瀬（solver）

3129 (+4)

・vs. taisa（solver）

4670 (+1545)

一之瀬solverは「いくつかの頂点を適当に選んで削除してしまい、葉に隣接する頂点は削除する」ということをしており、輪の部分で一つ偶奇の正しい方を選んで削除すると自動的にすべて正しい方を選ぶことになるため、ほぼ最適解を導いていた。元のグラフにおいて葉を切る貪欲が効かないように輪の形にしていたが、部分的に頂点を削除したときには葉が発生することになることがポイントだった。

一方、TAISA solver(２近似アルゴリズム+山登り)に対しては、一つの小グラフが11頂点と小さかったことによって山登り法での辺の入れ替えにおける近傍内に有効なものがより少なくなり、より大きな差を生み出すことに成功していた。

終了後に、二部グラフであることが指摘された。二部グラフの最小頂点被覆は最大フローに帰着され、辺の重みがすべて1であるからO(N√M) で解ける。そのため、N,M <= 10^4であれば十分高速に厳密解が求められる。

TAISA

N=10000, M=5627

想定解：3500

テストケースを作る際、相手のsolverの出す解のサイズを大きくすることも重要だが、自分の用意する想定解のサイズが十分に小さいことも必要である。TAISAのグラフは、N=20の小グラフをランダムに生成してその最小頂点被覆を求め、それらを最適性が失われないように繋げて連結にしたものである。

・vs. 一之瀬（solver）

3500 (+0)

・vs. Segtree（solver）

3500 (+0)

どちらのsolverの解も想定解とぴったり同じサイズになった。

元のN=20の小グラフが簡単なものであり、貪欲法によって最適解が求まるものだったのだと思われる。

本人は0を下回らなかった時点で目的は達成できていると主張していた。

総合結果

1位　一之瀬　+1843pt

2位　Segtree　+705pt

3位　TAISA　-2548pt

solverもグラフも強かった一之瀬が優勝した。

TAISAのグラフはN=20のグラフの中で良いものを引き当てることができれば健闘しただろう。

振り返り

頂点被覆と独立集合は補集合の関係にあり、最小頂点被覆と最大独立集合が同じ問題であることが知られている。

最大独立集合問題はNP困難であるが、厳密解を求めるアルゴリズムであって、指数の底が小さく、実際にはより高速に動作することが期待されているものが存在する。
指数時間アルゴリズム入門 | PPT

はじめは速く動作することを期待してこれを書いてしまおうかと思ったが、実際には全員が小さなグラフをパスやサイクル状に繰り返すという方針を取っており、そのようなグラフでは10^4頂点では実行が終わらないところだった。このアルゴリズムの「次数が大きなものから選ぶか選ばないか決める」というパートで2^{小グラフの個数} の分岐ができてしまうため、一番小グラフの個数が少なかった一之瀬グラフでも2^99回規模のDFSの呼び出しが必要になる。

逆に、大きな構造としてパスやサイクルに近いということは、木幅が小さいということが推測されるだろう。木幅が小さなグラフに対しては、木分解を行った上でDPを行うという、木幅を定数として線形時間の厳密アルゴリズムが知られている。
木幅と線形時間アルゴリズム - blogoid

N,M <= 10000 という制約となった時点で参加者が作るグラフの木幅が小さいことが期待されるため、木分解上のDPを書くという戦略も有効だったかもしれない。