この記事は理情 Advent Calendar 2024 - Adventar の2日目の記事として書かれました。

ちなみに1日目の記事は無いらしいです。

はじめに

一之瀬、ひらきち、Segtreeの３名でじゃんけんAI大会を行った。

大会といっても、競技性をしっかり考えてレギュレーションを組んだり全身全霊で競争をするというものではなく、ゆるくプログラムを書いて遊ぼうという会である。

ルール

それぞれの人が、じゃんけんAIプログラムを書く。

じゃんけんは人間対AIで行われ、100回じゃんけんを繰り返す。

AIプログラムは対戦が始まってから相手の出した手の情報に応じて手の出し方を変えることができる。

詳細

人間 vs AI の形の総当たり戦を行う。（N人の場合、N(N-1) 回の対戦が行われる。）

それぞれの対戦では、google spreadsheet上でじゃんけんを100回行う。

google spreadsheet 上で対戦を行うことによって、プロンプト形式で対戦する場合に比べて、人間側が過去の手を確認しやすくなっている。

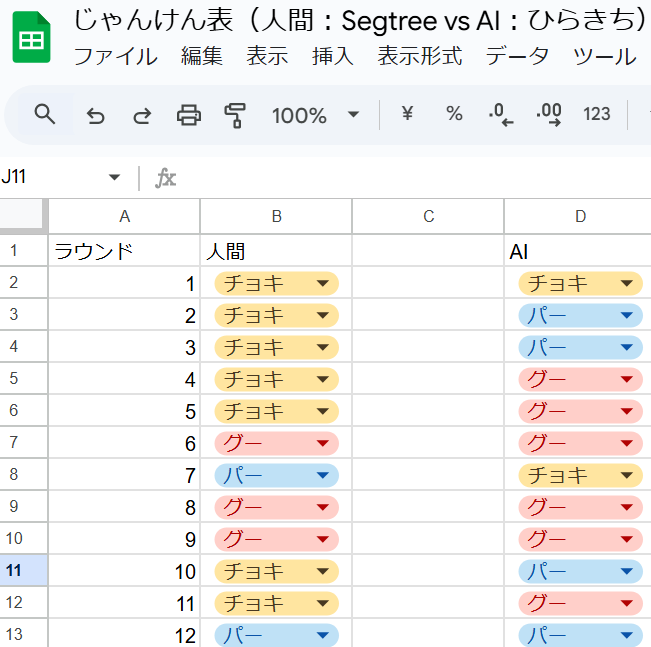
AIの勝利数 + 人間の勝利数によって順位を決める。

勝利数のみによって順位が決まるため、複数人のプレイヤーが「お互いが対戦するときは50勝50敗0分になるようにしよう」などと約束すると順位が上がってしまうので、それが禁止された。

追加ルール：裏工作禁止

各AIの特徴と対戦結果

各参加者が作ったAIの特徴と、そのAIと人間の対戦結果をまとめる。

一之瀬AI

相手の手を統計的に処理

相手が出した手、手の変化のしかたの傾向をカウントし、それに応じて手を出す。

・vs. ひらきち（人間）　人間側があまりに偏った手を出したことによって、AIが同じ手をずっと出すようになってしまい、人間側に手を読まれてしまった。ずっとパーを出していたらしい。　25-48（人間 +23）

・vs. Segtree（人間）　これも同様に、人間側の手が偏っていたことによって、AIが似たような手をずっと出してしまい、人間側に手を読まれてしまった。　29-40（人間 +11）

ひらきちAI

相手の手の出し方に特定の特徴があったらそれを読んでアンチパターンを送る。主に前の手との差分に注目していた。有限オートマトン形式だった。

・vs. 一之瀬（人間）　なぜか人間側は自分のAIで打っていたらしい　34-36（人間 +2）

・vs. Segtree（人間）　「負けた後は自分に負ける手を出す」のような法則を人間側が読んで優位に立ってはいたが、同じことをずっと続けているとAI側が法則を破ってくるという仕組みになっておりやや手強かった。　31-42（人間 +9）

Segtree AI

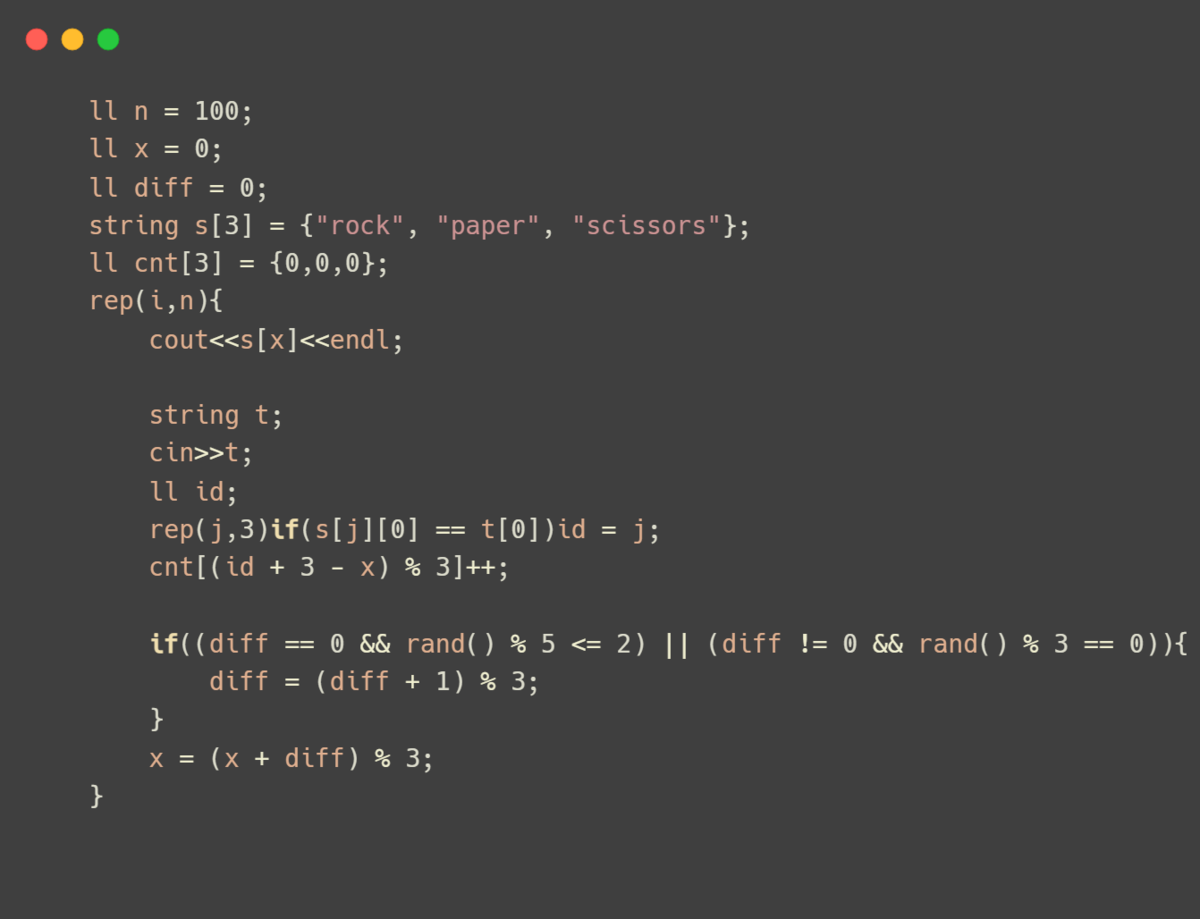
これまでの対戦結果の履歴が使えることを無視し、相手の手によらず一定の手の列を出す。

mod 3で見た時の前の手と現在の手の差分が0 -> 1 -> 2 -> 0 ... と一定時間ごとに変化するようにした。

人間の雑な予測に対するアンチパターンになり、ランダム以上に勝利数を稼ぐことを狙った。

・vs. 一之瀬（人間）　なぜか人間側は自作のAIで打っていたらしい　38-31（AI +7）
・vs. ひらきち（人間）　出力がConstantであることをうっかりもらしてしまい、人間が100回常にグーを出していた。　AIの生成した列に偶然チョキが多かったので、人間の勝ちが多くなった。　29-37（人間 +8）

総合結果

1位：ひらきち　150勝　132敗　118分

2位：Segtree　149勝　128敗　123分

3位：一之瀬　128勝　167敗　105分

1勝の差でひらきちが優勝した。

一之瀬AIに対する人間の勝数で大きな差が付いたようだ。

一之瀬AIは一行変えることによって相手の偏りに釣られて自分が偏ってしまうことを防ぐことができ、改良が見込まれるらしい。

考察

6戦のうち5戦で人間側が勝利しており、「人間がAIの挙動を読んで勝利する」ということが多かったことが分かる。

このとき人間が行っていたことはどのように解釈すれば良いか、プログラムで書くとすればどのようになるのか？という自然な疑問が生まれる。

万能じゃんけんAI

プログラムMが万能じゃんけんAIであるとは、

「あるクラスに属する任意のAIプログラムM'に対して、ある手数N (=f(M,M') )が存在して、MとM'を対戦させたときにN手以降で相手に全て勝つ」

ことを言う。

いくつかの対戦相手AIプログラムのクラスに対して、万能じゃんけんAIが存在するかを議論する。

相手のAIプログラムに時間制限がある場合

相手のAIプログラムについて「あるステップ数 k が存在して k ステップ以内に次の手を出す」ということが保証されている場合、そのようなクラスに対しては万能じゃんけんAIが存在する。（1ステップをどのように取るかには様々な方法があるが、例えばチューリングマシンへ帰着したときの1操作を1ステップとすればよい。）

構成

（あるチューリング完全な言語において）単純な方からプログラムを順に見ていき、相手のプログラムとしてこれまでの情報と矛盾しない候補を一つ管理していく。「実際にプログラムを実行し、k ステップ以内に結果を返さなかった場合や、出した手がこれまでの情報と矛盾したら現在の候補を棄却して次の候補に進む」ということを繰り返す。

相手のAIプログラムもしくはそれと今後の一切の実行において等価なプログラムに有限時間で辿り着くため、ある有限のタイミング以降では相手の手を完全に予測することができ、勝つことができる。

相手には時間制限があり、自分には時間制限が無いことがポイントである。

自分に一定の時間制限が付いていてもその値が十分に大きければ同様のプログラムが組めるが、どの程度まで時間制限を縮められるかは言語やステップ数の取り方依存である。ただし、時間制限が自分と相手で等しかった場合には不可能であることが示せる。（後述の議論と同様）

相手のAIプログラムのクラスに万能じゃんけんAI自身が含まれないことがポイントである。

相手のAIプログラムに有限時間で停止する以外の条件が無い場合

一定の時間制限があった場合には「実際にプログラムを実行し、時間制限まで待って、その結果出した手がこれまでの情報と矛盾したら次の候補に進む」ということができたが、一般の場合には停止しないプログラムが候補として挙がっていたときに、実際に何秒まで待てば良いかが決められないため、そのようなことができない。

このクラスに対して万能じゃんけんAIが存在しないことが簡単に証明できる。

不可能性の証明

万能じゃんけんAIプログラム自身もこのクラスに属する。そのため、二つの万能プログラムM1, M2どうしを対戦させることができる。f(M, M') をその手数以降 M'に対してMが常に勝ち続けるある手数とする（定義参照）。max( f(M1,M2), f(M2,M1) ) 手以降で、M1がM2に勝利し、M2がM1に勝利することになるが、これは矛盾。

結論

人間も万能じゃんけんAIと同様に、相手のプログラムやその挙動として考えられる候補を実際の挙動をもとに順に絞っていくというような戦略を取っており、これは素朴な統計的なプログラムに対して優位な戦略だったと言える。相手に完全に勝ち切る「万能じゃんけんAI」は、対戦する二者が対等な条件であれば存在せず、一手に掛けられる時間の差が十分にあれば時間が長い側にのみ存在する。